Tak jak statystyki czy wykresy mogą przekłamywać rzeczywistość, tak i oszukiwać mogą mapy, z których co dzień korzystamy. Jeśli jednak poznamy matematykę za mapami ukrytą, nie damy się tak łatwo wyprowadzić w pole - tłumaczy matematyczka dr Paulina Rowińska.
Dr Paulina Rowińska, absolwentka Imperial College London, jest popularyzatorką matematyki. Niedawno ukazała się po angielsku jej książka Mapmatics: How We Navigate the World Through Numbers. W książce tej bierze na warsztat różne mapy i w angażujący sposób opisuje ciekawe matematyczne zagadnienia z tym związane.
Coraz większa jest już świadomość, że statystyki czy infografiki, z którymi się stykamy, mogą kłamać. Ale podobnie jest z mapami! A przecież na ich podstawie też podejmujemy różne decyzje. Warto o tym pamiętać! - mówi w rozmowie z PAP dr Paulina Rowińska.
Prognoza pogody w telewizji, wybór trasy dojazdu na wakacje, aplikacje pokazujące, gdzie jest nasza przesyłka, mapki ilustrujące wydarzenia na świecie, a nawet "geograficzne" memy z cyklu "widać zabory" czy "najpopularniejsze imiona w różnych państwach". Nie ma dnia, kiedy nie korzystamy z map. Zwykle są to mapy, których nie opracowaliśmy sami, ale zrobił je ktoś inny. Czy powinniśmy im w pełni zaufać? Jeśli dowiemy się, chociaż pobieżnie, jaka matematyka stoi za poszczególnymi mapami, trudniej będzie nas oszukać - podsumowuje Rowińska. W swojej książce m.in. tłumaczy dlaczego - i jak - różne mapy oszukują.
"Oszustwa" na mapie
W tworzeniu map świata problemem nie do pokonania jest m.in. to, że trójwymiarowej sfery - powierzchni kuli - nie jesteśmy w stanie odwzorować bez zniekształceń na dwuwymiarowej kartce. Najprościej zobaczyć to, kiedy obieramy pomarańczę - skórki nie możemy płasko rozłożyć na stole. Żeby to się dało zrobić, trzeba ją przedrzeć w wielu miejscach - porównuje matematyczka. Udowodnił to już w swoim "twierdzeniu wybornym" (Theorema Egregium) Carl Friedrich Gauss. W mapach świata zawsze pojawią się więc jakieś przekłamania - w kątach, odległościach, powierzchniach, bo trzeba znaleźć jakiś naginający rzeczywistość sposób, żeby rzutować tę nieszczęsną sferę (czy raczej geoidę) na kartkę.
Dr Paulina Rowińska jako przykład podaje stosowaną na każdym kroku mapę Merkatora. Ona powstała do nawigacji i do tego rzeczywiście dobrze się nadaje: zachowane są w niej kąty. Nie nadaje się jednak do tego, żeby w szkole uczyć się z niej świata, bo zaburzone są choćby proporcje powierzchni kontynentów - ocenia.
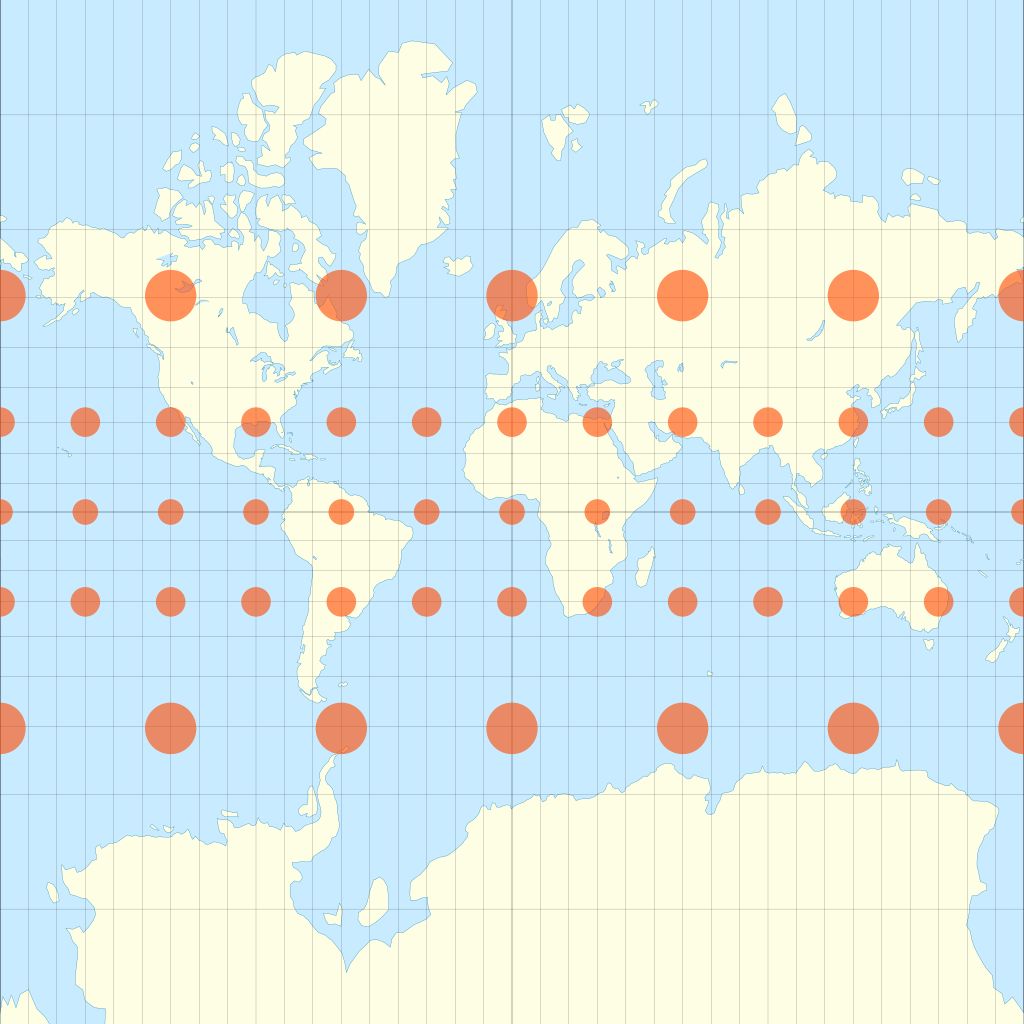
Rys. 1. Odwzorowanie Merkatora. Żródło: Justin Kunimune/ Wikipedia/ CC BY-SA 4.0.
Na odwzorowaniu Merkatora (tzw. walcowym równokątnym) południki i równoleżniki w każdym miejscu mapy przecinają się pod kątem prostym. A północ zawsze jest na górze. Kosztem takiego przedstawienia kuli jest to, że zniekształcone są powierzchnie: położone bliżej biegunów Antarktyda, Rosja czy Grenlandia wydają się gigantyczne, a umiejscowienie bliżej równika Afryka czy Ameryka Południowa - nieproporcjonalnie małe.
Rowińska w swojej książce proponuje rozwiązać quiz, aby się przekonać, jak trudne jest porównanie powierzchni różnych obszarów, zwłaszcza, jeśli częściej mamy do czynienia z oszukańczymi mapami, a nie choćby ze zwykłym globusem.
Pytana o to, jakie odwzorowania lepiej niż Merkatora nadają się do obeznania się ze światem, podpowiada, że może to być np. wiernopowierzchniowe odwzorowanie Galla-Petersa, które również zniekształca kształty kontynentów, ale dobrze oddaje ich powierzchnię
Badaczka poleca też odwzorowanie Winkel tripel lub projekcję Robinsona, które zniekształcają wprawdzie po trochu powierzchnię, i kierunek, i dystans, ale za to w ogólnym rozrachunku i tak dają niezłe pojęcie o układzie świata. Projekcja Robinsona jest moim zdaniem jedną z piękniejszych - komentuje.
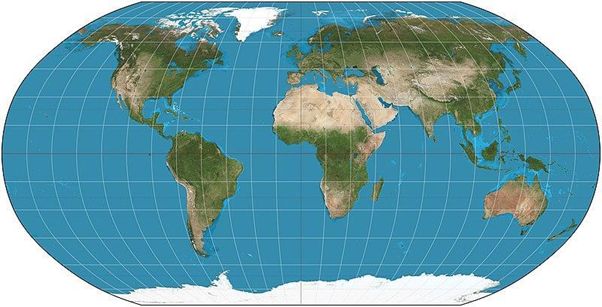
Rys 2. Odwzorowanie Robinsona; Żródło: Strebe, Wikimedia, CC BY-SA 3.0.
"Oszustwa" samolotowe
Rowińska zwraca też w swojej książce uwagę na to, jak dziwnie wyglądają na płaskich mapach trasy samolotów pokonujących długie trasy. No bo dlaczego samolot lecący z Warszawy do leżącego na południe od niej Los Angeles przelatuje nad Szwecją, Norwegią ,Grenlandią i Kanadą? Kiedy patrzy się na tę trasę na mapie Merkatora, wydaje się to zbędne nadkładanie drogi: czy nie prościej lecieć nad Niemcami i Francją? Trzeba jednak pamiętać, że najkrótsza trasa na płaskiej mapie wcale nie musi być najkrótszą trasą na sferze. Wystarczy rozciągnąć sznureczek na globusie (albo miarkę np. w aplikacji Google Earth, która na dłuższych dystansach pokazuje kulistość Ziemi), żeby się przekonać, że rzeczywiście płaska mapa może tu łatwo wprowadzić w błąd.
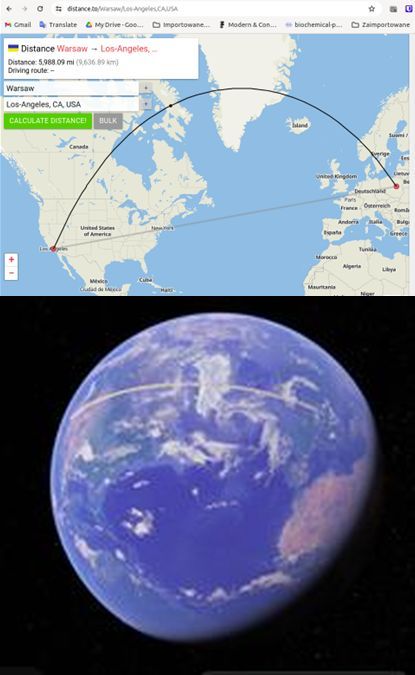
Rys 3. Na płaskiej mapie najkrótsza droga z Warszawy do Los Angeles wydaje się przecinać Niemcy, kanał La Manche i Nowy Jork. Tymczasem na kulistej Ziemi okaże się to zbędnym nadkładaniem drogi: najkrótsza droga wiedzie na północny zachód: przecina Szwecję, Norwegię, Grenlandię i Kanadę. Źrodło: distance.to; Google Earth
"Oszustwa" w komunikacji miejskiej
Porcja matematyki przyda się też, by lepiej zrozumieć, jak wykiwać nas mogą mapy komunikacji miejskiej.
Ikoniczna stała się już mapa metra londyńskiego Henry’ego Becka. Linie metra biegną tu tylko w pionie, poziomie i pod kątem 45 stopni, a kolejne stacje jednej linii są od siebie jednakowo oddalone. Na podobnych zasadach skonstruowana jest mapa transportu szynowego w Warszawie.
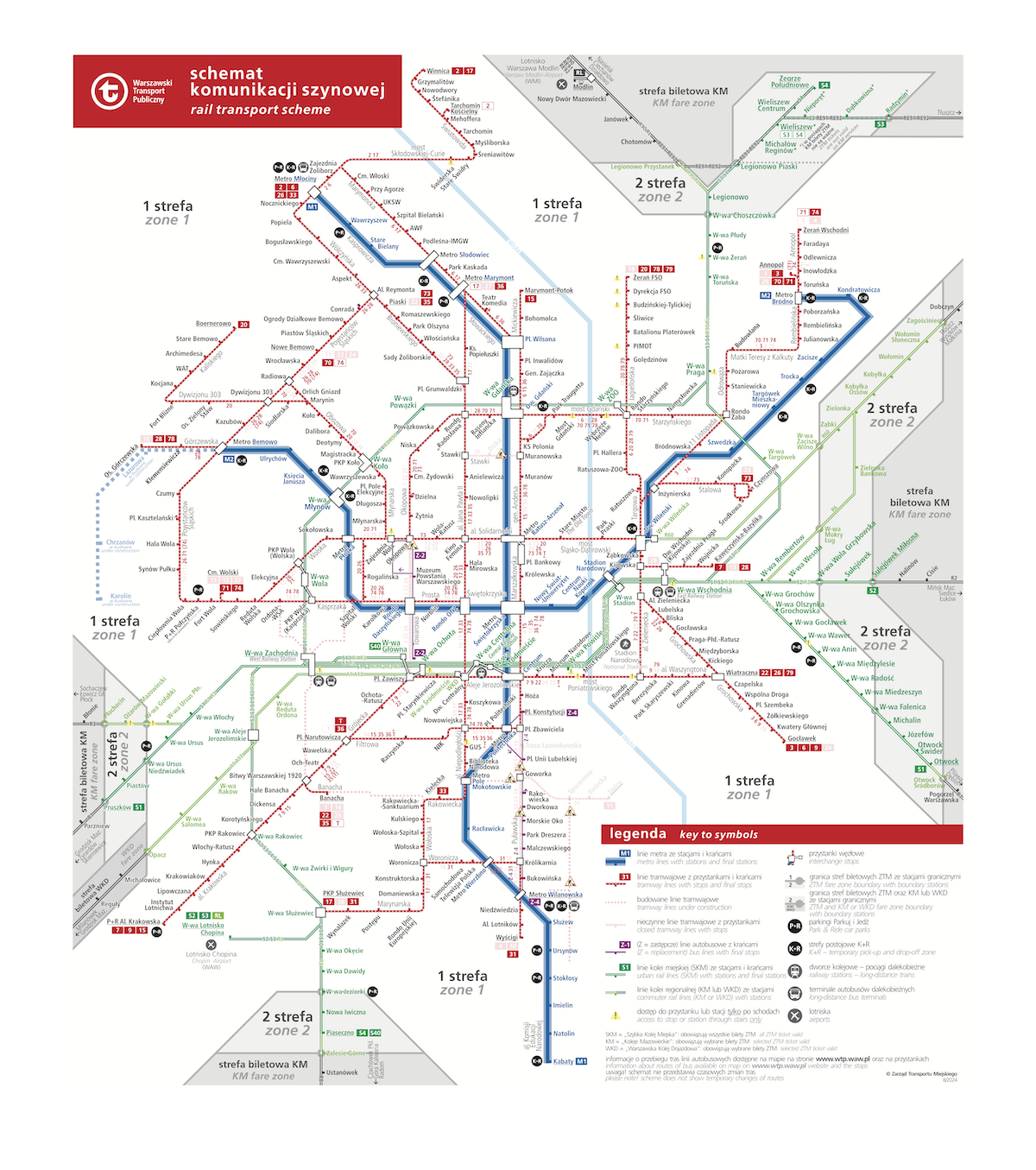
Rys 4. Schemat komunikacji szynowej Warszawskiego Transportu Publicznego. Mapa pokazuje dobrze trasy poszczególnych linii i możliwości przesiadek, ale nie oddaje wiernie odległości. Warszawski Gocław zdaje się być położony dziwnie blisko Józefowa, a Kabaty wyglądają jakby były dalej od centrum niż Piaseczno. Źródło: Zarząd Transportu Miejskiego.
Taka mapa jest rzeczywiście klarowna, jeśli chcemy gdzieś dojechać, ale nie zależy nam na czasie: zachowane są w niej kolejność przystanków i możliwości przesiadek. Poważnemu zniekształceniu uległy tu jednak odległości między punktami w mieście, kąty, pod którymi krzyżują się linie czy wielkości dzielnic.
I tu kłania się dział matematyki nazywany topologią - nauka, w której ściskanie, ugniatanie lub rozciąganie (bez rozdzierania i sklejania) nie zmienia właściwości obiektów. Takie deformacje, nazywane homeomorfizmami (od greckiego homoios oznaczającego „podobny, równy” i morphē oznaczającego „kształt”), zachowują połączenia między punktami. Jeśli dwa punkty były blisko siebie wcześniej, to nadal będą względnie blisko siebie po homeomorfizmie - pisze matematyczka. I wyjaśnia, że na tym właśnie polega wyjątkowość mapy Becka. W tego typu mapach znaczenie ma topologia, a nie topografia - pisze dr Rowińska.
Mapy w polityce
Mapy nie tylko oszukują, ale mogą zostać użyte do oszukiwania - i to na dużą skalę - choćby po to, by wygrywać wybory.
Tzw. gerrymandering to technika takiego wyznaczania granic okręgów wyborczych, aby kandydaci wybranej partii mogli wygrać - uzyskać jak największą liczbę mandatów wyborczych. Jeśli zna się preferencje wyborców w różnych okolicach, to np. można tak ustalić granice okręgów wyborczych, aby "upchnąć" przeciwników w jak najmniejszej liczbie okręgów wyborczych. I w ten sposób zostawić dla siebie wygraną w pozostałych okręgach wyborczych. Bywa też tak, że rozdmuchuje się granice okręgów, by przeciwnicy byli tam w mniejszości. Wszystkie te taktyki zmierzają do jak największego marnowania głosów przeciwników, a więc zapobiegają temu, by konkurenci mieli wpływ na wybory. A to przecież zaprzeczenie zasadzie demokracji, która mówi, że każdy głos tak samo się liczy - pisze Rowińska.
A w rozmowie z PAP dodaje, że w USA pracuje wiele grup matematyków, które dopracowują algorytmy, by okręgi wyznaczać sprawiedliwie.
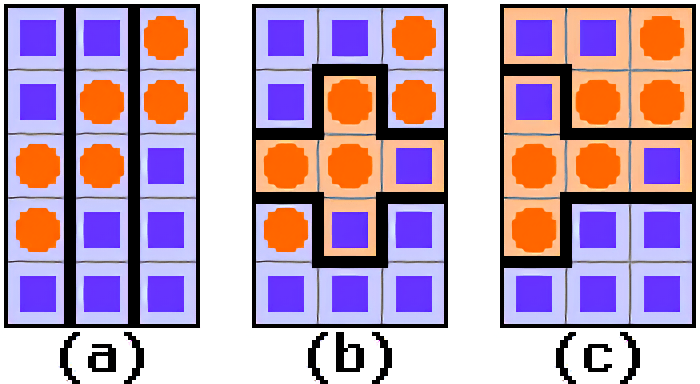
Rys 5. Jeśli w wyborach większościowych mamy: 6 zwolenników pomarańczy i 9 zwolenników śliwek, to nie jest jasne, kto zdobędzie większość w wyborach - wszystko zależy od rozdysponowania granic okręgów wyborczych. można tak ustawić granice obwodów, żeby mandat zdobyło a) 3 kandydatów śliwek i 0 pomarańczy b) 2 kandydatów śliwek i 1 pomarańczy c) dwóch kandydatów pomarańczy i 1 - śliwek. Źródło: Cmglee, Wikipedia.
Warto samemu wyrobić sobie opinię na temat różnych map, poznać ich plusy i minusy, i dowiedzieć się, z czego one wynikają - namawia dr Rowińska.
Konsekwencje związane z bezkrytycznym stosowaniem map mogą być błahe - ktoś nie trafi na czas w miejsce, którego szuka lub nadłoży drogi w czasie wycieczki. Ale i poważne: w wyborach zwycięży nieuczciwa partia...
(Źródło: Nauka w Polsce, Ludwika Tomala, PAP)



















