Gdy w dzieciństwie razem z moją młodszą siostrą grałam w karty i kości, segregowałam guziki, nie przypuszczałam, że kiedyś stanie się to ważną częścią mojej pracy zawodowej. Być może tym spontanicznym zabawom zawdzięczam to, że lubiłam matematykę. Dziś gram w karty, kości z moimi uczniami i zachęcam do tych zabaw rodziców.
Matematyka to sztuka myślenia, należy więc już od najmłodszych lat pobudzać i rozwijać myślenie dzieci, dawać im wiele okazji do eksperymentowania, ale także uczyć istoty poszczególnych pojęć. Nabywanie kolejnych matematycznych umiejętności jest w końcu niczym budowanie papierowego łańcucha na choinkę – na jednych budowane są inne. Ważna jest kolejność wprowadzania pojęć matematycznych. Kluczową ideą nauczania matematyki jest uczenie się przez działanie, doświadczanie i komunikację. Bardzo ważne jest, by umożliwić uczniom samodzielne zdobywanie, odkrywanie wiedzy poprzez uczenie się przez gry, zabawy, techniki myślenia twórczego, doświadczanie.
W swojej pracy terapeutycznej stosuję gry i zabawy z wykorzystaniem kości, kart, domina, guzików, plansz do gier. Tak powstały autorskie pomoce dydaktyczne „Matematyczne rozgrywki” oraz „Mnożę i dzielę” (wyd. Annał). Podczas ćwiczeń zaangażowane są wszystkie zmysły dziecka. Kształtuje się pojęcie liczby naturalnej w podstawowych jej aspektach, umiejętności matematyczne takie jak przeliczanie, dodawanie, odejmowanie, mnożenie i dzielenie oraz doskonalą się funkcje percepcyjno-motoryczne. Wielokrotne powtarzanie operacji matematycznych na wymienionych pomocach prowadzi do wytworzenia schematów myślowych dziecka. W terapii wykorzystuję też zabawy ruchowe połączone z wykonywaniem działań matematycznych. Skutecznym sposobem na zapamiętywanie pojęć matematycznych są skojarzenia, z których chętnie korzystam. Poprzez rozgrywanie gier dzieci hartują swoją odporność emocjonalną. Uczą się pokonywania trudności, przestrzegania reguł, radzenia sobie z przegraną. Samo uczestnictwo w grze jest dla nich źródłem radości.
Udział w zabawach i grach matematycznych redukuje lęk przed uczeniem się matematyki, doskonali umiejętności rachunkowe dzieci i rozwija logiczne myślenie. Zdobyte sprawności będą przydatne nie tylko w uczeniu się matematyki, ale również w innych obszarach edukacji szkolnej.
Poniżej zaprezentowane są przykładowe ćwiczenia pochodzące z „Matematycznych rozgrywek” i „Mnożę i dzielę” (Z. Olejniczak, J. Wójcicka). Więcej ćwiczeń pokażę na warsztacie, który odbędzie się 2 marca 2018 roku podczas konferencji "Fascynujący świat matematyki" w Collegium Da Vinci w Poznaniu. Serdecznie zapraszam.
1. Krzyżówki liczbowe
Pomoce: karty z liczbami od 1 do 10, żetony
Uczestnicy otrzymują po 5 kart. Pozostałe karty leżą na środku stołu zakryte w stosie. Odkrywamy jedną kartę. Pierwszy gracz dokłada do niej taką kartę, żeby suma liczb była równa 10 lub mniej. Kolejne osoby dokładają karty w pionowych lub poziomych rzędach tak, aby suma nie przekroczyła 10. Po każdym wyłożeniu dobieramy kartę ze stosu, aby gracz miał przed sobą zawsze 5 kart. Gracz, który dopełni do 10 dostaje punkt i zabiera żeton. Gra toczy się do wyczerpania kart. Wygrywa osoba, która zebrała najwięcej punktów.
2. Bingo karciane
Pomoce: karty z liczbami od 1 do 10, kostki
Gracze losują po 9 kart, które układają odkryte przed sobą po trzy karty w trzech rzędach. Pozostałe karty leżą zakryte w stosie. Pierwsza osoba rzuca dwiema kostkami. Oblicza sumę wyrzuconych oczek na kostkach. Kto ma taką liczbę na swojej karcie, odwraca ją. Gracze odkrywają karty ze stosu na zmianę. W jednym ruchu wolno odwrócić tylko jedną kartę. Osoba, która pierwsza będzie miała odwrócone 3 karty ułożone w jednej linii – poziomej, pionowej lub ukośnie mówi „Bingo” i wygrywa grę.
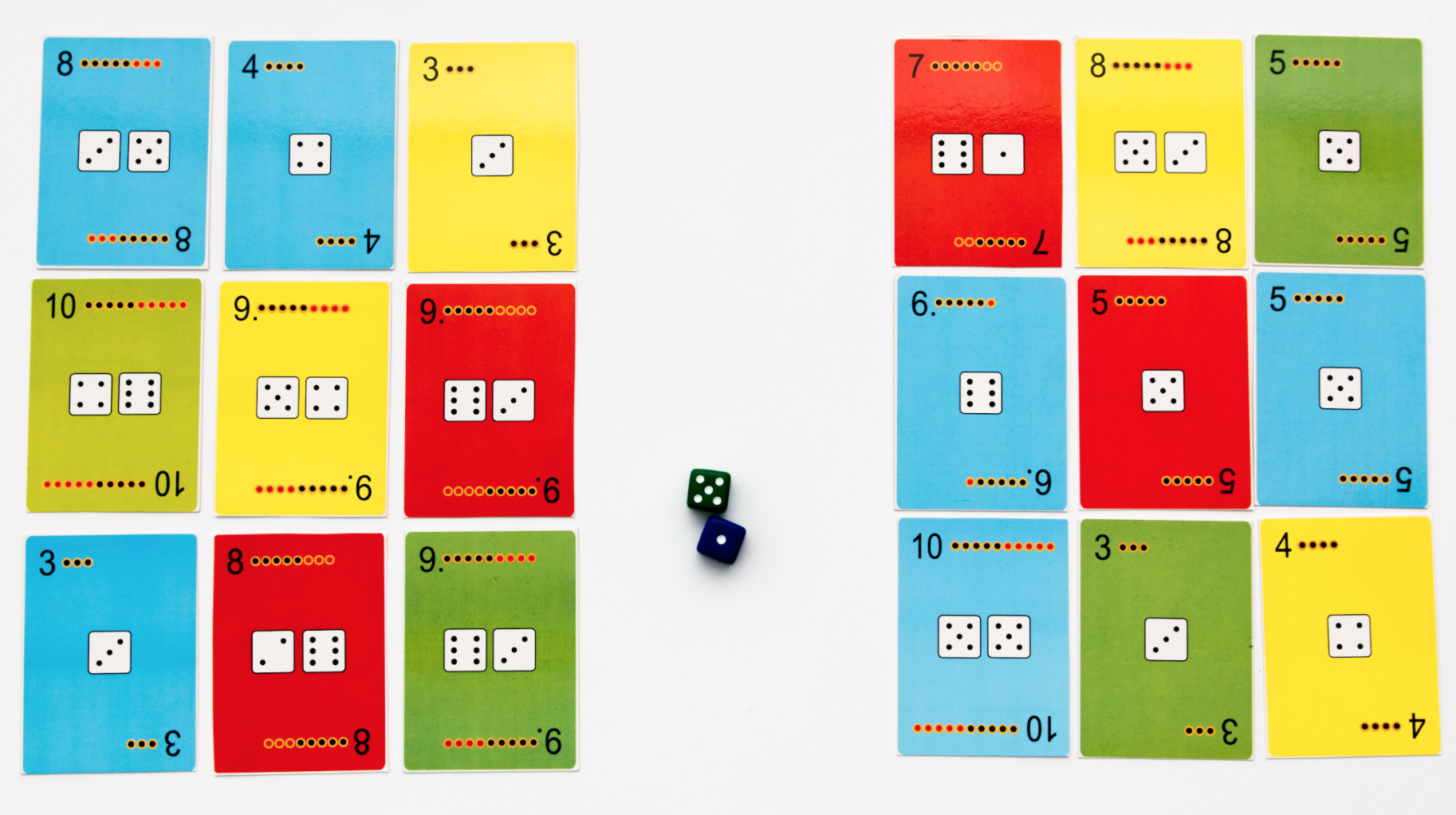
3. Grupowanie kostek
Pomoce: kostki, żetony
Każdy z graczy rzuca 15 kostek. Następnie grupuje tak, aby suma kropek na kostkach wynosiła 10. Kto ułoży więcej dziesiątek dostaje punkt (żeton). W przypadku ułożenia tej samej liczby dziesiątek punkty otrzymują obaj gracze. Grę powtarzamy kilkakrotnie. Wygrywa ten, kto zdobędzie więcej punktów.

4. Dopełnij do sześciu
Pomoce: domino
Płytki domina mieszamy i rozdzielamy po równo między uczestników. Leżą odkryte przed graczami. Pierwsza osoba kładzie dowolną płytkę na środku. Drugi gracz dokłada do niej płytkę tak, aby suma kropek na stykających się polach sąsiednich płytek była równa 6 (można ustalić inną liczbę). Płytki można dokładać z każdej strony. Gra toczy się do momentu, gdy zostaną ułożone wszystkie płytki domina lub nie można już żadnej dołożyć. Wygrywa osoba, która pierwsza pozbędzie się swoich płytek lub zostanie z mniejszą liczba płytek.

5. Memo - mnożenie (Wariant 1)
Pomoce: wybrane karty z działaniami - mnożenie (przez 2 i 3 lub 4 i 5, 6 i 7, 8 i 9) - oraz karty z liczbami
Wszystkie karty tasujemy i układamy zakryte na stole w równych rzędach np. cztery rzędy po 5 kart. Pierwszy gracz odkrywa dwie dowolne karty i sprawdza, czy stanowią one parę tzn. działanie jest równe wynikowi. Jeżeli tak, zabiera je. Jeżeli nie - zostawia odkryte na stole. Następny gracz odkrywa kolejne dwie karty. Sprawdza, czy wśród wszystkich odkrytych kart może dobrać pary. Zabiera wszystkie znalezione pary kart. Następna osoba odkrywa kolejne dwie karty i gra toczy się do wyczerpania kart. Wygrywa osoba, która zebrała więcej par.
6. Domino
Pomoce: domino
Płytki domina tasujemy i rozdzielamy po równo między uczestników. Leżą odkryte przed graczami. Pierwsza osoba kładzie dowolna płytkę na środku. Drugi gracz dokłada do niej płytkę tak, aby na stykających się polach było to samo mnożenie: zapisane liczbami i przedstawione na kostkach. Płytki można dokładać z każdej strony. Wygrywa osoba, która pierwsza pozbędzie się swoich płytek.
7. Układaj działania
Pomoce: kostki, żetony
Każdy z graczy rzuca 10 kości, następnie grupuje je wg liczby kropek – osobno jedynki, osobno dwójki, trójki itd. Zapisują działania i oblicza. Kto ma większy wynik , otrzymuje żeton. Wygrywa ten, kto ma więcej żetonów.
Działanie 2 x 2 + 4 x 5+ 4 x 3= 4+20+12=24 + 12 = 36

Notka o autorce: Joanna Wójcicka - pedagog i specjalista w zakresie diagnozy i terapii dzieci i młodzieży z trudnościami w uczeniu się matematyki, edukator. Terapeuta w Poradni Psychologiczno Pedagogicznej nr 1 w Łodzi. Założyciel Arkana Centrum Wspierania Edukacji i Rozwoju. Prowadzi szkolenia dla nauczycieli i rodziców, słuchaczy studiów podyplomowych oraz studentów z zakresu diagnozy i terapii trudności matematycznych. Współautorka gier edukacyjnych „Matematyczne rozgrywki”, „Mnożę i dzielę” (wyd. Annał) oraz publikacji „Polubić matematykę” (wyd. AHE).



















